Bab 1 : Fungsi
1. Fungsi ialah sejenis hubungan khas yang mana setiap objek dalam domain mempunyai hanya satu imej dalam kodomain.
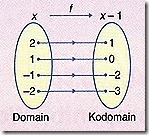

Hubungan satu dengan satu Hubungan satu dengan satu
ialah fungsi ialah fungsi
2. Fungsi nilai mutlak ditakrifkan oleh

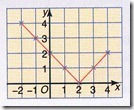
Graf fungsi nilai mutlak

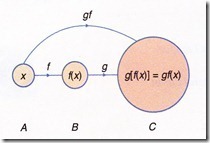
3. Jika f ialah suatu fungsi yang memetakan set A kepada set B dan g ialah suatu fungsi yang memetakan set B kepada set C, maka gf ialah fungsi gubahan f diikuti dengan g yang memetakan set A terus kepada set C.
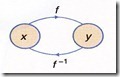
4. Jika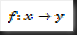 ialah suatu fungsi yang memetakan x kepada y, maka songsangannya ditandakan sebagai f-1. Fungsi songsang ialah suatu fungsi yag memetakan y kembali kepada x.
ialah suatu fungsi yang memetakan x kepada y, maka songsangannya ditandakan sebagai f-1. Fungsi songsang ialah suatu fungsi yag memetakan y kembali kepada x.

1. Fungsi ialah sejenis hubungan khas yang mana setiap objek dalam domain mempunyai hanya satu imej dalam kodomain.


Hubungan satu dengan satu Hubungan satu dengan satu
ialah fungsi ialah fungsi
2. Fungsi nilai mutlak ditakrifkan oleh


Graf fungsi nilai mutlak
3. Jika f ialah suatu fungsi yang memetakan set A kepada set B dan g ialah suatu fungsi yang memetakan set B kepada set C, maka gf ialah fungsi gubahan f diikuti dengan g yang memetakan set A terus kepada set C.

4. Jika

Bab 2 : Persamaan Kuadratik
1. Bentuk am persamaan kuadratik ialah
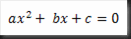 yang mana:
yang mana:
1. Bentuk am persamaan kuadratik ialah
a, b dan c = pemalar
a ≠ 0
x = pembolehubah
2. Suatu persamaan kuadratik ax2 + bx + c = 0 dapat diselesaikan dengan
menggunakan kaedah:
3. Persamaan kuadratik dapat dituliskan sebagai

4. Bagi persamaan kuadratik ax2 + bx + c = 0,

5. Syarat untuk jenis punca persamaan kuadratik ialah
6.

3. Persamaan kuadratik dapat dituliskan sebagai
4. Bagi persamaan kuadratik ax2 + bx + c = 0,

5. Syarat untuk jenis punca persamaan kuadratik ialah

6.

Bab 3 : Fungsi Kuadratik

2. Nilai maksimum atau minimum bagi suatu fungsi kuadratik f(x) = ax2 + bx + c dapat dicari dengan menggunakan kaedah penyempurnaan kuasa dua, iaitu dengan mengungkapkan ax2 + bx + c dalam bentuk a(x + p)2 + q.
3. Apabila a > 0, fungsi a(x + p)2 + q mempunyai nilai minimum. Nilai minimum itu ialah q dan ini berlaku apabila x = –p.

4. Apabila a > 0, fungsi a(x + p)2 + q mempunyai nilai maksimum. Nilai maksimum itu ialah q dan ini berlaku apabila x = –p.

5. Bagi fungsi kuadratik f(x) = ax2 + bx + c = a(x + p)2 + q, persamaan paksi simetri ialah
6. Ketaksamaan kuadratik dapat diselesaikan dengan menggunakan kaedah lakaran graf seperti berikut.

2. Nilai maksimum atau minimum bagi suatu fungsi kuadratik f(x) = ax2 + bx + c dapat dicari dengan menggunakan kaedah penyempurnaan kuasa dua, iaitu dengan mengungkapkan ax2 + bx + c dalam bentuk a(x + p)2 + q.
3. Apabila a > 0, fungsi a(x + p)2 + q mempunyai nilai minimum. Nilai minimum itu ialah q dan ini berlaku apabila x = –p.

4. Apabila a > 0, fungsi a(x + p)2 + q mempunyai nilai maksimum. Nilai maksimum itu ialah q dan ini berlaku apabila x = –p.

5. Bagi fungsi kuadratik f(x) = ax2 + bx + c = a(x + p)2 + q, persamaan paksi simetri ialah
6. Ketaksamaan kuadratik dapat diselesaikan dengan menggunakan kaedah lakaran graf seperti berikut.

Bab 5 : Indeks dan Logaritma
1. Hukum-hukum indeks ialah:
2. Indeks pecahan : 3. Indeks negatif :


4. Jika ax = y dengan keadaan a > 0, a ≠ 1, maka x ialah logaritma bagi y kepada asas a, iaitu
5. 6.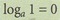

7. Hukum-hukum logaritma ialah

8.

9. Logaritma sesuatu nombor pada suatu asas tertentu boleh ditukarkan kepada asas yang lain dengan menggunakan rumus-rumus

10. Persamaan indeks
Jika an = bn, dengan keadaan a > 0, b > 0 atau a < 0, b < 0, maka
11. Persamaan logaritma
Jika maka x = y.
maka x = y.
1. Hukum-hukum indeks ialah:

2. Indeks pecahan : 3. Indeks negatif :
4. Jika ax = y dengan keadaan a > 0, a ≠ 1, maka x ialah logaritma bagi y kepada asas a, iaitu
5. 6.
7. Hukum-hukum logaritma ialah

8.
9. Logaritma sesuatu nombor pada suatu asas tertentu boleh ditukarkan kepada asas yang lain dengan menggunakan rumus-rumus

10. Persamaan indeks
Jika an = bn, dengan keadaan a > 0, b > 0 atau a < 0, b < 0, maka
11. Persamaan logaritma
Jika
Bab 6 : Geometri Koordinat
1. Jarak = 2. Titik tengah =

3. Koordinat titik yang membahagi secara dalam tembereng garis dengan nisbah m : n ialah
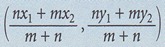
4. Luas segitiga =
5. Luas sisiempat =
6. Kecerunan = @
@
7. Persamaan garis lurus ialah

9. Terdapat 3 jenis syarat yang menentukan persamaan lokus satu titik bergerak P(x,y):
(a) Jaraknya dari satu titik tetap, Q(x1, y1) ialah satu pemalar (k).
(b) Jaraknya dari dua titik tetap, Q(x1, y1) dan R(x2, y2) adalah sama.
(c) Nisbah jaraknya dari dua titik tetap, Q(x1, y1) dan R(x2, y2) ialah m : n.
1. Jarak = 2. Titik tengah =
3. Koordinat titik yang membahagi secara dalam tembereng garis dengan nisbah m : n ialah
4. Luas segitiga =
5. Luas sisiempat =
6. Kecerunan =
7. Persamaan garis lurus ialah
- jika kecerunan, m dan satu titik, (x1, y1) diberi,
- jika dua titik, (x1, y1) dan (x2, y2) diberi,
- jika pintasan-x, a dan pintasan-y, b diberi,

9. Terdapat 3 jenis syarat yang menentukan persamaan lokus satu titik bergerak P(x,y):
(a) Jaraknya dari satu titik tetap, Q(x1, y1) ialah satu pemalar (k).

(b) Jaraknya dari dua titik tetap, Q(x1, y1) dan R(x2, y2) adalah sama.

(c) Nisbah jaraknya dari dua titik tetap, Q(x1, y1) dan R(x2, y2) ialah m : n.

Bab 7 : Statistik
1.

2. Jika setiap cerapan dalam set data ditambah atau ditolak dengan satu nilai pemalar k, maka
3. Jika setiap cerapan dalam set data didarab dengan satu pemalar k, maka
4. Jika setiap cerapan dalam set data ditambah atau ditolak dengan satu nilai pemalar k, maka
5. Jika setiap cerapan dalam set data didarab dengan satu pemalar k, maka
6. Apabila dua set data, X dan Y digabungkan, maka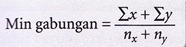

1.


2. Jika setiap cerapan dalam set data ditambah atau ditolak dengan satu nilai pemalar k, maka

3. Jika setiap cerapan dalam set data didarab dengan satu pemalar k, maka

4. Jika setiap cerapan dalam set data ditambah atau ditolak dengan satu nilai pemalar k, maka

5. Jika setiap cerapan dalam set data didarab dengan satu pemalar k, maka

6. Apabila dua set data, X dan Y digabungkan, maka

Bab 8 : Sukatan Membulat
1. Rumus penukaran darjah kepada radian ialah
2. Rumus penukaran radian kepada darjah ialah
3.
4.
5.
1. Rumus penukaran darjah kepada radian ialah

2. Rumus penukaran radian kepada darjah ialah

3.

4.

5.

Bab 9 : Pembezaan
1. Terbitan pertama bagi suatu fungsi y terhadap x ialah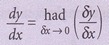
2, Jika y = uv, maka
3. Jika![clip_image002[4] clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhMuJuIwx1CFwVbHaE0c10OgVHz25kQoIZllnciQegzBSnMdEbYgSWnlgvr_LyqMA7dbVTW4fhhjk7sUn1bsdCKFcQEawOY9ekwMknHF0wuCvj3xUD3YZZRONQS2J43HMjzIWeXaXzk7n0/?imgmax=800) , maka
, maka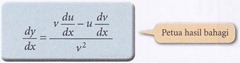
4. Jika y = k[f(x)]n, maka
5. Jika y = f(u) dan u = g(x), maka

6. Persamaan tangen pada titik (x1, y1) ialah
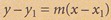
7. Persamaan normal pada titik (x1, y1) ialah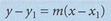

8. Pada titik pusingan,

9. Pada titik maksimum, 10. Pada titik minimum,

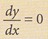
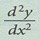
 adalah negatif. adalah positif.
adalah negatif. adalah positif.
11. Masalah Maksimum dan Minimum
12. Kadar Perubahan yang Terhubung
13. Perubahan Kecil
14. Penghampiran
1. Terbitan pertama bagi suatu fungsi y terhadap x ialah
2, Jika y = uv, maka

3. Jika
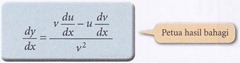
4. Jika y = k[f(x)]n, maka

5. Jika y = f(u) dan u = g(x), maka

6. Persamaan tangen pada titik (x1, y1) ialah
7. Persamaan normal pada titik (x1, y1) ialah
yang mana
8. Pada titik pusingan,
9. Pada titik maksimum, 10. Pada titik minimum,
dan tanda dan tanda
11. Masalah Maksimum dan Minimum

12. Kadar Perubahan yang Terhubung

13. Perubahan Kecil

14. Penghampiran

Bab 10 : Penyelesaian Segitiga
1.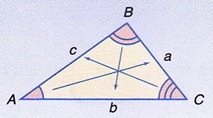
Petua sinus diberi oleh
atau

2. Petua Sinus melibatkan Kes Berambiguiti

3. Petua Kosinus diberi oleh

4. Luas segitiga ABC
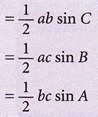
5. Geometri Tiga Matra
(a)

(b)


1.

Petua sinus diberi oleh
atau
2. Petua Sinus melibatkan Kes Berambiguiti

3. Petua Kosinus diberi oleh

4. Luas segitiga ABC
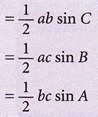
5. Geometri Tiga Matra
(a)

(b)




good note cikgu..well done..tq so much
ReplyDeletewow! this is awesome. :)
ReplyDeleteMohon ambil nota. Untuk kegunaan sendiri dan juga kpd anak sendiri. Syukran jazilan. Moga Cikgu sentiasa hebat kerana orang yang cintakan ilmu tidak akan kedekut untuk berkongsi ilmu dengan sesiapa jua..Welldone!
ReplyDeletetq so much yeahh
ReplyDeleteUr welcome
DeleteAssalam, t.ksh.
ReplyDeletemmng bgus,awesome, nota ringkas tapi padat, teks yang mnrik... sya bgi 200%...dn 5bntng :)
ReplyDelete1000% dan 50bintang
Deleteterbaiiik la...tq
ReplyDeletemohon izin copy nota nie...harap halalkan ilmu utk pembelajaran saya
ReplyDeletesaya juga... TQ <3
DeleteThis comment has been removed by the author.
DeleteThanks n good job sir ..mohon menggunakanya
ReplyDeleteCikgu tolong bgi cara nk buat
ReplyDeleteTQ dan mohon halalkan utk saya gunakannya.
ReplyDeletemuchos gracias..its awesome. it might help many students.
ReplyDeleteTQ.... halalkan ya, sy guna. Semoga tuhan membalas jasa baik cikgu.
ReplyDeleteAssalamualaikum terima kasih cikgu, mintak gunakan nota ini untuk belajar yaa tq
ReplyDeleteMinta halal ilmu ni ya cikgu harap tuhan membalas jasa cikgu
ReplyDeleteAssalamualaikum cikgu.terima kasih cikgu untuk nota ini. mohon halalkan ya untuk di sebarkan. terima kasih
ReplyDeletetq
ReplyDeletemudah difahami
Good thanks
ReplyDeletehaarap halal kan ilmu ni ye..saye nk copy
ReplyDeleteAssalamualaikum..mohon izin untuk dicopy dan disebarkan ilmu ini ya.. terima kasih banyak banyak..
ReplyDeleteTq. -chw
ReplyDeleteTerima kasih
ReplyDeleteTerima kasih
ReplyDeletemohon share
ReplyDeletethank you very much
ReplyDeletethis is a perfect notes, Thanks, May allah bless you :)
ReplyDeleteThe perfect one notes.. Thanks
ReplyDeleteThank for notes . Can u make video ???
ReplyDelete[sorry im bad in english ]
wow! this notes is so USEFUL to me, isn't it? thanks for this notes! :)
ReplyDeleteTHANKS.. AMAT MEMEBANTU .. Thanks you =]
ReplyDeletesaya copy . terima kasih atas perkongsian ni . semoga diberkati dunia akhirat
ReplyDeletebyk boleh betolkan.............saya tegur jgn marah....
ReplyDeleteok lar tu.Gud job.Terbaik cikgu dan sgt membantu.
Deletesaya copy ya sir, mintak halalkan segalanya. doakan saya dipermudahkan menjawab addmath ya .aminn :) terima kasih . #spm2016
ReplyDeleteTq sir...harap sir halalkan ilmu yng diberi..#spm2016
ReplyDeletemohon nota cikgu , moga ilmu dihalalkan..
ReplyDeleteTq. Sangat membantu my F5 students. Hanya Allah yang membalas jasa cikgu
ReplyDeletemohon guna nota cikgu, moga dihalalkan
ReplyDeleteMohon copy..
ReplyDeleteTerima kasih..
hope jdy nota yg berguna..n thanks cikgu
ReplyDeleteMohon guna nota dear,nota yg padat 😂
ReplyDeleteThanks
Mohon izin Cikgu untuk menyalin nota untuk kegunaan anak saya. Terima kasih.
ReplyDeleteAsslamulaikum Cikgu/Tuan
ReplyDeleteSaya seorang pelajar di SMK Gelang Patah.
Bolehkah saya guna nota cikgu/tuan untuk aplikasi android/ios
yang saya bangunkan.Url blog ini akan diletakkan di bahagian nota dan Credit.
Sekian,Terima kasih
izinkan saya copy ilmu ni, :) sangat membantu
ReplyDeleteminta izin untuk copy dan guna yer..moga manfaatnya sampai pada saya dan cikgu,In Shaa Allah
ReplyDeletethank you teacher, i really love this blog ! <3
ReplyDeletewow.. ni memang terbaik arh..
ReplyDeleteThis is really helpful thanks
ReplyDeletenota sepintas lalu yg padat lagi gempak. copy bleh?
ReplyDeleteMohon share nota ni. Thx u moga murah rezeki di dunia akhirat.
ReplyDeleteMohon copy % guna nota cikgu ya..
ReplyDeleteassalamualaikum..sy buat rujukan ngajor hometusyen...mohon halalkan ye..hihi.. email sy: nadoranaceyra@gmail.com
ReplyDeleteBig thumbs up����
ReplyDeleteCopy for my own use.Harap halalkan
ReplyDeletemohon share nota ni ye. tq :)
ReplyDeleteThanks. Saya ada print sc dan share dgn murid. Mohon halal kan pnggunaannya. Tqvm
ReplyDeletemohon halal ilmu ye cikgu moga murah rezeki cikgu dan keluarga aamiinn...
ReplyDeletemohon guna nota ye cgu..terima kasih..semoga Allah merahmati cgu sekeluarga.amin
ReplyDeleteExcellent Cikgu,Tapi jika Bab 4 Persamaan Serentak diDetailkan dengan gambar rajah lagi baik,Terima Kasih Cikgu,
ReplyDeletewahhh.. sungguh membantu.. terima kasih dan mohon halalkan saya menyalin nota ini ya.. :)
ReplyDeletemohon izin utk guna bahan cikgu utk mengajar kpd student sy ye
ReplyDeleteTq cikgu
ReplyDeleteDiberi f (x) = 2 tan x, cari imej bagi 0°.
ReplyDeletemohon utk saya gunapakai nota dan soalan2 ni ya utk anak saya
ReplyDeleteTerima kasih. Saya minta izin untuk guna ya
ReplyDeletethank you
ReplyDeletethank you for this note..... doakan saya agar lulus dengan cemerlang di SPM nanti....
ReplyDeletebapak ah...selama ni aku belajar bodoh bodoh jer tengok buku teks gan rujukan semua..padahal dh ade dh pun blog pasal addmath..
ReplyDeletesaya bagi 10000000% dan 5 bintang dan lebih...
Besar jasa cikgu buatkan nota ni , terima kasih tak terhingga ♡
ReplyDeleteuseful notes,im gonna show it to my friends also !! tysm author
ReplyDeleteIts show me how to do well in addmath tq!
ReplyDeleteSangat membantu😁
ReplyDelete#addmath A+ di hujung jari..terima kasih banyak banyak cikgu..
ReplyDeleteminta izin share,berkati ilmu ni
ReplyDeletethank u si much .....it helps me for my exam
ReplyDeleteKebanyakannya pelajar form 3 tahun 2019 ni dah belajar hampir semua bab dari add-math ni, patutlah susah...
ReplyDeletethankyou cikgu , halalkan ilmu ini ya .. semoga berjaya duniawi ukhrawi
ReplyDeletethanks it can help my revision
ReplyDeletebagus..tq
ReplyDeleteTerima kasih atas nota tersebut,sangat membantu
ReplyDeletepizza
ReplyDeleteNota cg blh membantu sy n ank sy dlm musim pkp ni. Nota ringkas n senang utk difahami. Terima kasih cg.
ReplyDeleteThanks.. Lengkap notanya.. Mohon share dengan anak anak didik
ReplyDeleteTerima kasih cikgu..saya nak minta izin untuk salin dan gunakan sebagai rujukan untuk peperiksaan SPM
ReplyDeleteTerima kasih cg...sgt membantu sy dlm addmath...moga cikgu murah rezeki slalu^^
ReplyDelete�� 5000+ SEAT SAHAJA LAGI !!! ��
ReplyDeleteCALLING�� FOR ALL STUDENTS�� YANG PERLUKAN BIMBINGAN✍�� DAN BANTUAN�� DALAM MATEMATIK!��
Seminar pada 20 & 21 Februari�� hari Sabtu kita akan belajar Algebra�� hari Ahad kita akan belajar Add Math�� dalam topik-topik Index�� Fungsi�� dan asas-asas Add Math�� yang semua rasa susah�� Jangan risau�� seminar ni enjoy habissss�� no tension�� no stress��
Daftar ���� segera ��% PERCUMA‼️
Tak Percaya ⁉️⁉️
YA‼️
��% PERCUMA‼️
Masa dah tiba⏳ untuk kita rasa Matematik tu senang ✅ Jangan buang masa lagi�� JOM DAFTAR CEPAT��
1. Tekan links di bawah ��������
http://www.aster.edu.my/seminar
2. Pilih "TIKET"
3. Isi maklumat diri dan penjaga
4. Isi REFERRAL UNIK ID di ruangan nombor 6⃣
5. Semak e-mail yang anda masukkan untuk maklumat lanjut dan link telegram untuk workbook
DONE ✅
Mana pulak nak dapat REFERRAL UNIK ID ni ?��
Haaaaa��
©opy atau salin siap² REFERRAL UNIK ID di bawah ������������
BCO-OO43
Astervengers, bertindak!����
#teamLISHAH��
atau
#teamNANANA��
Pssssttt�� jgn lupa share tau�� dekat family�� dan kwn² �� semoga bermanfaat untuk semua..
Mohon halalkan ilmu yg digunakan utk anak saya.. semoga cikgu dimurahkan rezeki yg diberkati.
ReplyDeleteterima kasih cikgu sy nk exam harini sangat membantu
ReplyDeleteTrial spm esok....semoga dipermudahkan...
ReplyDeleteBurik
ReplyDelete'Adiyat minta maaf
ReplyDelete